Подбор сечения нижней части колонны

Сечение нижней части колонны – сквозное, состоящее из 2-х ветвей, соединенных решеткой. Высота сечения hН = 1500мм. Подкрановую ветвь колонны принимаем из широкополочного двутавра, наружную – составного сварного сечения из 3-х листов. Определяем ориентировочное положение центра тяжести.

Принимаем

Zo = 6см; h0 = h – Z0 = 150 – 6 = 144 см.

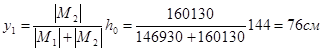
Определяем усилия в ветвях:

- в подкрановой ветви:

- в наружной ветви:

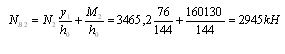
расстояния от центра тяжести сечения колонны до центра тяжести соответствующих ветвей.

Для подкрановой ветви

Задаемся

Определяем требуемую площадь ветвей и назначаем сечение нижней части колонны.

по сортаменту принимаем двутавр №70Б1; AB1 = 162 см2; iу = 27,9 см; iх = 5,31 см.

Для шатровой ветви:

R=215МПа = 21,5кН/см2 (сталь Вст3кн2, листовой проат),

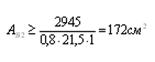
Для удобства прикрепления элементов решетки, просвет между внутренними гранями полок принимаем таким же, как в подкрановой ветви (663 мм).

Толщину стенки швеллера () принимаем равной 16 мм; высота стенки из условия размещения сварных швов – 710 мм.

Требуемая площадь полок:

из условий местной устойчивости полки швеллера:

Принимаем: tn = 16 мм; bn = 220 мм; Ап=35,2 см2

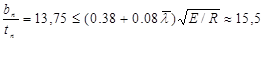
Геометрические характеристики ветви

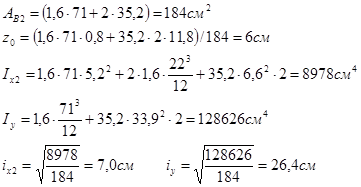
Уточняем положение центра тяжести сечения колонны:

h0 = hH – Z0 = 150 – 6 = 144 см

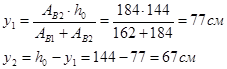
Отличие от первоначально принятых размеров мало, поэтому усилия в ветвях не пересчитываем.

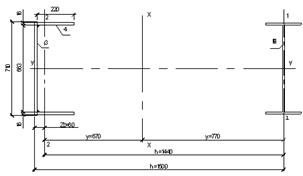
Проверяем устойчивость ветвей:

- из плоскости рамы (относительно оси у – у) ly = 1620 см.

Подкрановая ветвь:

Наружная ветвь:

Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы определяем требуемое расстояние между узлами решетки:

Принимаем lB1 = 300 см, разделив нижнюю часть колонны на целое число панелей.

Проверяем устойчивость ветвей в плоскости рамы (относительно осей х1 – х1 и х2 – х2)