Наблюдения за горизонтальными смещениями сооружений

Величины смещений находятся по разности значений ординат (нестворностей), измеренных в двух циклах.

Нестворность определяют различными методами, из которых наиболее распространены методы подвижной марки и малых углов. Для задания створной линии применяют струнные и оптические способы, а также способы, основанные на принципах физической оптики. Струнный способ предусматривает использование натянутой стальной струны различного диаметра, оптический – зрительных труб большое увеличение (теодолиты, нивелиры, автоколлимационные системы, специальные алиниометры).

В методе подвижной марки величина нестворности определяется непосредственно. Для этого в точке А (рис. 5, а) устанавливается оптический прибор, коллимационная плоскость которого ориентируется по марке в точке В и задает створную линию. Подвижная марка, установленная в точке С, вводится в створ. Положение подвижной марки, когда мишень ее находится в створе, фиксируется по отсчетному устройству марки. Если известен отсчет, когда ось мишени совпадает с точкой С, то Нестворность qC может быть вычислена как разность отсчетов при положении марки в точке С и в створе АВ. При возможности поворота марки на 180° Нестворность может быть получена как полуразность отсчетов для двух положений марки при введении ее в створ.

В методе малых углов Нестворность q определяется путем измерения малого угла α (рис. 5, б) между линией створа и направлением на точку С и расстояния S. Величина нестворности вычисляется по формуле qC=Sα/ρ.

Для створов значительной протяженности с большим числом определяемых точек на створе в зависимости от условий измерений применяют различные схемы (программы) наблюдений. Простейшая из них – схема общего створа (рис. 6, а), когда нестворности всех точек определяются относительно общего створа между концевыми (опорными) точками створа. В схемах частных (пересекающихся) (рис. 6, б) и последовательных (рис. 6, в) створов нестворности измеряются между определяемыми точками относительно этих створов.

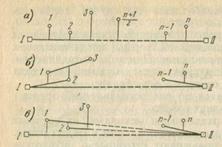
Рис.6. Схемы створных измерений

Так, схема последовательных створов предусматривает определение нестворности ∆1 точки 1 от створа

1 – II, ∆2 точки 2 от створа

1 – II, ∆3 точки 3 от створа

2 – II и т.д. В схеме частных створов нестворность ∆1 точки 1 определяется от створа 1 – 2, ∆2 точки 2 от створа 1 – 3, ∆3 точки 3 от створа 2 – 4 и т.д. В обеих схемах нестворности q относительно общего створа могут быть получены лишь путем соответствующих вычислений, зная расстояния S между всеми точками.

В общем случае, когда расстояния между определяемыми точками не равны между собой, нестворности всех n точек относительно общего створа могут быть найдены из решения системы следующих линейных уравнений:

для схемы последовательных створов

; . . . . . . . . . (7)

;

;

для схемы частных створов

;

; . . . . . . . . . . . (8)

;

.

На практике расстояния между точками створа стараются сделать равными. В этом случае нестворность qi любой определяемой точки i в схемах последовательных и частных створов может быть вычислена соответственно по формулам